User guide¶
This guide covers the basics of using dislib, and details on the different algorithms included in the library.
dislib provides two major programming interfaces: an API to manage data in a distributed way, and an estimator-based interface to work with different machine learning models. The distributed data API is built around the concept of distributed arrays (ds-arrays), and the estimator-based interface has been inspired by scikit-learn.
The term estimator-based interface means that all the machine learning models in dislib are provided as estimator objects. An estimator is anything that learns from data given certain parameters. dislib estimators implement the same API as scikit-learn, which is mainly based on the fit and predict operators.
The typical workflow in dislib consists of the following steps:
- Reading input data into a ds-array
- Creating an estimator object
- Fitting the estimator with the input data
- Getting information from the model’s estimator or applying the model to new data
An example of performing K-means
clustering with dislib is as follows:
import dislib as ds
from dislib.cluster import KMeans
if __name__ == '__main__':
# load data into a ds-array
x = ds.load_txt_file("/path/to/file", block_size=(100, 100))
# create estimator object
kmeans = KMeans(n_clusters=10)
# fit estimator
kmeans.fit(x)
# get information from the model
cluster_centers = kmeans.centers
It is worth noting that, although the code above looks completely sequential, all dislib algorithms and operations are paralellized using PyCOMPSs.
How to run dislib¶
dislib can be installed and used as a regular Python library. However,
dislib makes use of PyCOMPSs directives internally to parallelize all the
computation. This means that applications using dislib need to be executed
with PyCOMPSs. This can be done with the runcompss or
enqueue_compss commands:
runcompss my_dislib_application.py
For more information on how to start running your dislib applications, refer to the quickstart guide.
Distributed arrays¶
Distributed arrays (ds-arrays) are the main data structure used in dislib. In essence, a ds-array is a matrix divided in blocks that are stored remotely. Each block of a ds-array is a NumPy array or a SciPy CSR matrix, depending on the kind of data used to create the ds-array. dislib provides an API similar to NumPy to work with ds-arrays in a completely sequential way. However, ds-arrays are not stored in the local memory. This means that ds-arrays can store much more data than regular NumPy arrays.
All operations on ds-arrays are internally parallelized with PyCOMPSs. The degree of parallelization is controlled using the array’s block size. Block size defines the number of rows and columns of each block in a ds-array. Sometimes a ds-array cannot be completely split into uniform blocks of a given size. In these cases, the bottom and right blocks will be smaller than the specified regular block size. Choosing the right block size is essential to be able to exploit dislib’s full potential.
Choosing the right block size¶
The ideal block size depends on the available resources and the application. The number of tasks generated by a dislib application is inversely proportional to the block size. This means that small blocks allow for higher parallelism as the computation is divided in more tasks. However, handling a large number of blocks also produces overhead that can have a negative impact on performance. Thus, the optimal block size will allow the full utilization of the available resources without adding too much overhead.
In addition to this, block size also affects the amount of data that tasks load into memory. This means that block size should never be bigger than the amount of available memory per processor.
Most estimators in dislib process ds-arrays in blocks of rows (or samples). This means that the optimal block size when using these estimators might be to have as many horizontal blocks as available processors. For example, in a computer with 4 processors, K-means (and other similar estimators) will usually fit a 100x100 ds-array faster using blocks of size 25x100 than using blocks of size 50x50, even though the number of blocks is 4 in both cases.
The diagram below shows how the K-means estimator would process an 8x8 ds-array split in different block sizes.
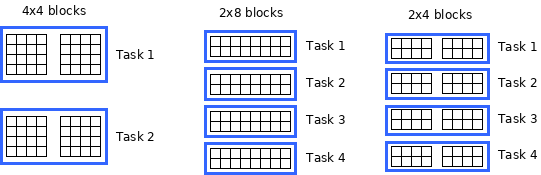
Using 4x4 blocks only generates 2 tasks, while using 2x8 blocks generates 4 tasks and provides more parallelism in a system with 4 processors. Using 2x4 blocks provides the same parallelism as 2x8 blocks, but has the overhead of dealing with five additional blocks. If we were only doing K-means clustering, 2x8 blocks would probably be the optimal choice in this scenario.
However, some estimators like
ALS benefit from having a uniform
number of blocks both vertically and horizontally. In these cases, it might
be better to split the ds-array in NxN blocks, where N is the number of
processors. This splitting strategy can be a good choice if you are not sure
on which block size to use in your application.
Below you will find more details on the parallelization strategy and data access pattern of each estimator. This can help you to define the appropriate block size in your application.
Another thing to take into account when choosing block size is task granularity. As said before, the number of tasks created by dislib is proportional to the number of blocks (and inversely proportional to block size). Also, block size is directly proportional to task duration or granularity (i.e., smaller blocks result in shorter tasks). This is relevant because, in distributed environments, task scheduling requires communicating with a remote computer and transferring some data, which has a significant cost. Thus, long tasks (big blocks) are typically more efficient than short tasks (small blocks).
For example, if the cost of scheduling a task in a remote computer is 5ms and the duration of that task is 2ms, running that task in a remotely is simply not worth the effort as we would be spending more time communicating than computing. Since task duration is directly related to block size, it is in general recommended to use big blocks rather than small ones.
Summary¶
To summarize, there is a trade-off between amount of parallelism, scheduling overhead and memory usage that highly depends on your platform. Nevertheless, these are the main ideas when choosing your block size:
- Ensure that a block of rows fits in the memory of a single processor.
- Define NxN blocks, where N is the number of processors you want to use.
- For small ds-arrays, it might be better to use N < number of processors and increase granularity at the cost of reducing parallelism.
Irregular blocks¶
Usually a ds-array cannot be divided into blocks of equal size. In this case, bottom-most blocks can be shorter than the regular block size, and right-most blocks can be narrower. When both dimension are not divisible by the desired block height/weight, bottom-right block is both shorter and narrower.
However, there is also a special case for sliced ds-arrays. If the performed slicing begins in middle of the block, this block is sliced and its new dimensions are kept as the top-left block instead of re-chunking the whole array. The resulting ds-array would then have the top and the left blocks smaller than the regular size blocks. Furthermore, it could also have the bottom and the right blocks smaller as well, depending on the original shape of the matrix, and the bottom/right bounds used in slicing. This optimization helps to avoid unnecessary and costly re-chunking of the ds-array.
Creating arrays¶
dislib provides a set of routines to create ds-arrays from scratch
or using existing data. The API reference contains the
full list of available routines. For example,
random_array can be used to create
a ds-array with random data:
import dislib as ds
x = ds.random_array(shape=(100, 100), block_size=(20, 20))
Another way of creating a ds-array is by reading data from a file. dislib
supports common data formats, such as CSV and SVMLight, using
load_txt_file and
load_svmlight_file.
Slicing¶
Similar to NumPy arrays, ds-arrays provide different types of slicing. The result of an slicing operation is a new ds-array with a subset of elements of the original ds-array.
Currently, these are the supported slicing methods:
x[i]- returns the ith row of x.
x[i,j]- returns the element at the (i,j) position.
x[i:j]- returns a set of rows (from i to j), where i and j are optional.
x[:, i:j]- returns a set of columns (from i to j), where i and j are optional.
x[[i,j,k]]- returns a set of non-consecutive rows.
x[:, [i,j,k]]- returns a set of non-consecutive columns.
x[i:j, k:m]- returns a set of elements, where i, j, m, and n are optional.
Resource allocation¶
All dislib tasks are allocated a specific number of computational resources. By default, each task receives one CPU. This number can be adjusted according to the specific needs of the program by setting the environment variable ComputingUnits before executing the script:
export ComputingUnits=8
The above example sets the number of CPUs available for each task to 8. This is specifically useful for algorithms (for example those implemented in NumPy) that automatically take advantage of fine-grained parallelism facilitated by a higher number of computing units.
Classification¶
The module dislib.classification includes
estimators that can be used for predicting the classes of unlabeled data,
after being fitted with data labeled with classes from a finite set. Each
estimator implements the fit method to build the model and the predict
method to classify new data.
The input of the fit method are two ds-arrays: a ds-array
x, of shape [n_samples, n_features] holding the training samples,
and a ds-array y of integer values, shape [n_samples], holding the
class labels for the training samples. The predict method takes a single
ds-array with the samples to be classified. These ds-arrays can be loaded
using one of the dislib.data methods.
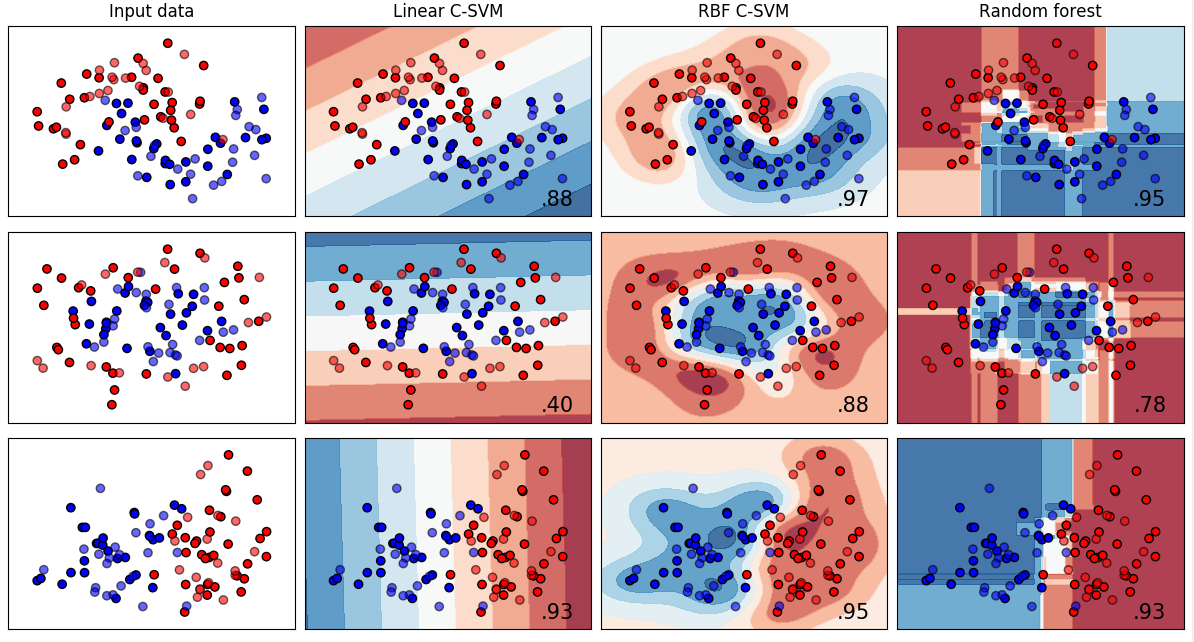
Comparision of classification methods:
Cascade SVM¶
The CascadeSVM
estimator implements a version of support vector machines that
parallelizes training by using a cascade structure [Graf05]. The algorithm
splits the input data into N subsets, trains each subset independently,
merges the computed support vectors of each subset two by two, and trains
again each merged group of support vectors. One iteration of the algorithm
finishes when a single group of support vectors remains. The final support
vectors are then merged with the original subsets, and the process is repeated
for a fixed number of iterations or until a convergence criterion is met. A
diagram of one iteration from Graf et al. can be seen below:
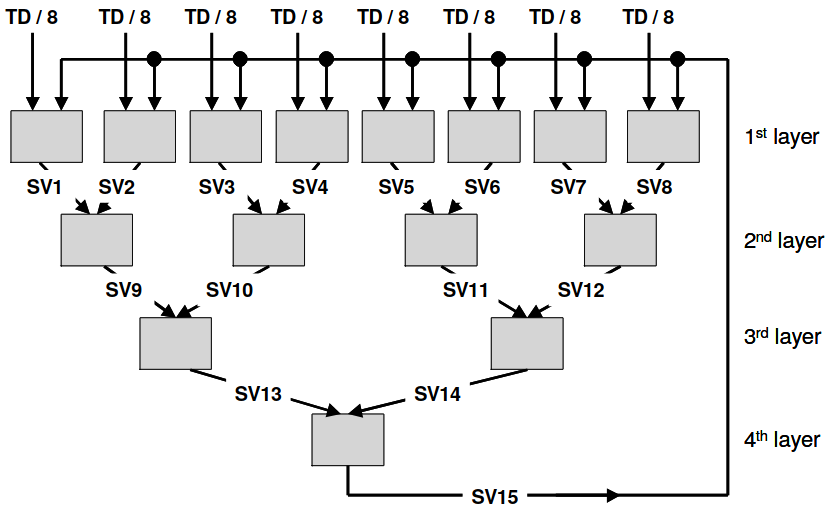
The fitting process of the CascadeSVM estimator creates the first layer of the cascade with the
different row blocks of the input ds-array. This means that the estimator
creates one task per row block at the first layer, and then creates the rest
of the tasks in the cascade. Each of these tasks use
scikit-learn’s SVC internally for training, and load a row
block in memory.
The maximum amount of parallelism of the fitting process is thus limited by the number of row blocks in the input ds-array. In addition to this, the scalability of the estimator is limited by the reduction phase of the cascade.
Random forest classifier¶
RandomForestClassifier
is a classifier that uses an ensemble of decision trees and aggregates their
predictions. The process of building each decision tree includes some
randomization in order to make them different. The accuracy of the joint
prediction can be greater than that of individual decision trees. One advantage
of Random Forests is that you cannot overfit by increasing the number of
trees. Several variations of random forests have been proposed and implemented.
A fundamental paper that has been cited extensively is [Bre01], which
describes the following method for classification problems:
For building each tree, the original sample set is replaced by a set of the same size, obtained by drawing with replacement (this method is called bootstrap aggregating or bagging). At each tree node, a certain number of random features is selected (random feature selection). The sample set is splitted in two according to the values of these features, and a metric called ‘Gini impurity’ is computed for every split. The Gini impurity measures how heterogeneous is one sample set with respect to the target variable. The split with the lowest ‘Gini impurity’ is selected, and the subsamples are propagated to the children nodes. The trees grown are not pruned.
Ensemble estimators can be implemented in an embarrassingly parallel pattern.
You can do this with scikit-learn’s RandomForestClassifier using a
joblib.parallel_backend and setting the n_jobs parameter. However, you
need to be able to load your data into memory for each processor or to use
memory mapped arrays, which can be tricky specially with a distributed backend.
In our implementation, the samples as a whole are written into a binary file
and accessed using memory maps (the COMPSs runtime manages the transfers to
other nodes when needed). We used this approach because the performance penalty
of using distributed data was too large. Storing the samples file and saving
the decision trees introduces a big load to the disk storage of all nodes. If
your execution fails because you reach your disk storage limits, you can try
reducing the number of trees or reducing their size by setting the
max_depth parameter. If this is not enough, you may consider reducing
the samples.
In order to get further parallelism, each decision tree is not necessarily
built in a single task: there are tasks for building just a subtree, just a
node or even just part of a node. You can use the distr_depth parameter to
control the number of tasks used for each tree. However, be aware that the
number of tasks grows exponentially when you increase distr_depth, and that
the task loads become very unbalanced. The fitted decision trees are not
synchronized, so the prediction is equally distributed.
The results of the RandomForestClassifier can vary in every execution, due to
its random nature. To get reproducible results, a RandomState (pseudorandom
number generator) or an int can be provided to the random_state
parameter of the constructor. This works by passing a seed (generated by the
master’s RandomState) to each task that uses randomness, and creating a new
RandomState inside the task.
References:
| [Bre01] | (1, 2) Random Forests L. Breiman, 2001 |
| [Graf05] | Parallel support vector machines: The cascade svm H. P. Graf, E. Cosatto, L. Bottou, I. Dourdanovic, and V. Vapnik, 2005 |
Clustering¶
The module dislib.cluster includes estimators that can
be used to perform clustering of unlabeled data. Each estimator implements
the fit and the fit_predict methods. The former fits the model, and
the latter additionally returns a ds-array of integer labels corresponding to
the different clusters over the training data.
Usually, the input is an array of shape [n_samples, n_features],
representing your data, that can be loaded using one of the dislib.data
methods. For the future Daura algorithm, the input will be a ds-array of
pair-wise distances of shape [n_samples, n_samples].
Comparision of clustering methods:

K-means¶
K-means is a clustering algorithm that finds a predefined number of clusters in a dataset based on the distance between data points. The algorithm typically begins with N random centers, where N is defined by the user, assigns each data point to their closest center to create the initial N clusters, and then updates the centers to the mean of all the data points in each cluster. This process is repeated for a number of iterations or until the centers do not suffer a significant change in the update.
The KMeans estimator implements
a parallel version of the K-means algorithm. This version of the algorithm
starts off with n_clusters random centers, assigns each data point to
their closest center, and computes the summation of all points assigned to
each center. This process is done by creating one task per row block in the
input ds-array to compute partial summations, and then performing a reduction
that adds up all data points assigned to each center. After this reduction,
the total summation is divided by the number of points assigned to each
cluster to compute the new centers. The process is repeated for max_iter
iterations or until convergence. The algorithm’s maximum parallelism is
equal to the number of row blocks in the input ds-array and each task needs
to load a row block in memory.
DBSCAN¶
DBSCAN is a clustering algorithm
that uses the neighbouring relations of the samples for determining the
clusters. It requires two parameters: the neighbouring distance eps,
and the minimum number of samples in a neighbourhood min_samples, which
define the clusters according to some rules.
A detailed explanation of this algorithm is out of the scope of this guide.
However, it is important to know that it is not completely deterministic, as
some border samples can be assigned to different clusters. There is also the
notion of noise, for samples that don’t belong to any cluster; in this
implementation, “noise” samples are given the special label value -1.
Many advantages and disadvantages can be suggested for DBSCAN. On the good
side, it can find regions of varied shapes, including non-convex regions,
and the number of regions is not fixed by the parameters. On the other side,
finding appropriate eps and min_samples can be challenging, and
there may be no pair that works well globally for all the clusters on your
data.
In our implementation, the samples are partitioned according to the regions of a multidimensional grid of the feature space. Then, for each region, the neighbours of each sample are computed, taking into account that there may be neighbours in the same region but also in other regions. This can be divided into multiple tasks for regions that contain many samples. A partial DBSCAN is performed for each region, and finally the clusters found in different regions are merged to create the final clusters. Some synchronizations are necessary, and the dependency graph of the generated tasks is complex, but enough parallelism is achieved to speed up some executions.
The parameters n_regions, dimensions and max_samples define the
workflow of the distributed execution, and it is very important to
understand them for working with large datasets. The first two define your
multidimensional grid. The regions of the grid shouldn’t be thinner than
eps, because that would mean having to compare to many regions to find
the samples neighbours, creating many data dependencies that slow down the
execution. For the same reason, you don’t want to partition along more than
a few dimensions either. On the other hand, you want a big number of regions
to achieve greater parallelism. Additionally, your data shouldn’t be
partitioned very unevenly, as it could cause strong load imbalances among
the tasks.
For some problems, it’s not possible to carry out all of the previous
recommendations at the same time, specially if your eps is not small or
the number of features is big, and it may mean that this implementation is not
the most appropriate. But if eps is relatively small and even partitions
can be made, this implementation can have a good scalability for big numbers
of samples.
Gaussian mixture¶
GaussianMixture fits a
gaussian mixture model that represents the distribution of the sample as the
sum of several gaussian components. The aim is to maximize the likelihood that
the obtained model describes the observed data. A fitted gaussian mixture
model can be used to generate new samples that follow the same distribution.
It can also be used for clustering, by assigning to each individual the
component with highest probability density at that point.
Our implementation is based on the sequential implementation in scikit-learn, which uses an iterative expectation–maximization (EM) algorithm. In the expectation step, given the gaussian components, membership weights to each component are computed for each element in the sample. In the maximization step, these memberships are used to compute the parameters of the gaussian components that maximize the likelihood. These iterations are repeated until a termination criteria is met: either the change of a certain indicator is below a convergence threshold, or the number of iterations reaches a given limit.
For distributing the execution, the samples are partitioned by row blocks. The expectation step of each iteration is computed in a map-reduce pattern, where the reduction is used as a termination criteria for the next iteration but it does not block the maximization step. The maximization step has two parts, the first one for updating the weights and the centers of the components, and the second one for updating their covariances. These parts are computed in successive map-reduce patterns, and this completes the iteration.
With the parameter covariance_type you can define the shape of the gaussian
components (see image). Internally, this is represented by a covariances
array whose shape depends on the covariance_type:
(n_components,) if 'spherical',
(n_features, n_features) if 'tied',
(n_components, n_features) if 'diag',
(n_components, n_features, n_features) if 'full'.
If the number of features of your data is big, the 'full' and 'tied'
options can be computationally more expensive. Moreover, the covariances
array is loaded into memory and processed as a single piece, so you could run
into memory problems. Our implementation is designed to scale on the number
of samples, but not on the number of features.
The EM algorithm can converge to a local optimum, and the results are sensible to the initialization. By default, this estimator uses KMeans to initialize the centers, which accelerates the execution. You can also provide your own parameters or use random initialization. It is a good idea to run the algorithm multiple times with different starting conditions, because it can converge to different local optima.
Daura¶
Daura is a clustering algorithm
that uses the distances between the samples and a cutoff value to find clusters
centered in one of the samples such that all of the members of the cluster are
within a cutoff radius from the center. Clusters are taken by size, from larger
to smaller, in a sequential and greedy way.
The fit method takes a ds-array of distances as input, which makes it different than other clustering estimators. Bear in mind that, although this ds-array is passed as a single parameter, it does not need to exist as a whole at once: it can be computed in PyCOMPSs tasks and processed by Daura block by block, and internally Daura only looks for the neighbouring relations and saves them.
This algorithm is inherently sequential, i.e., one cluster has to be found before you can start looking for the next one. Finding one cluster at a time is what has been parallelized. For this reason, this algorithm may not improve the performance of a sequential approach for small datasets. On the other hand, it can improve the memory management and the performance for larger datasets, or when there are few clusters.
Regression¶
Linear regression¶
LinearRegression
performs multivariate linear regression with ordinary least squares. The
model is: y = alpha + beta*x + err, where alpha is the intercept and beta
is a vector of coefficients. The goal is to choose alpha and beta that
minimize the sum of the squared errors. These optimal parameters can be
computed using linear algebra. First, if we want to have an intercept term,
x is extended with an additional ones column. Then, the coefficients are
given by inv(x.T@x)@x.T@y.
In our implementation, we compute x.T@x and x.T@y separately with
map-reduce patterns, partitioning the samples only by row blocks. Each rows
block of x is extended with the ones columns, if necessary, in the same
tasks that do the products. As we are using row blocks as a whole, without
vertical partitioning, the resulting x.T@x and x.T@y consist of a
single block each. Finally, the coefficients are computed in a single task
by solving a linear system with np.linalg.solve, avoiding the
unnecessary computation of the inverse matrix.
This implementation is designed for a good scalability for big numbers of
samples. However, it cannot give any additional scalability with respect to
the number of features, because we hold in memory the x.T@x matrix, of
shape (n_features, n_features) and process it as a single block.
(To have scalability for big numbers of features, we would need to integrate
this with a distributed implementation of a method for solving a system of
linear equations.)
Random forest regressor¶
RandomForestRegressor
is a regressor that uses an ensemble of decision trees and aggregates their
predictions. The process of building each decision tree includes some
randomization in order to make them different. The accuracy of the joint
prediction can be greater than that of individual decision trees. One advantage
of Random Forests is that you cannot overfit by increasing the number of
trees. Several variations of random forests have been proposed and implemented.
A fundamental paper that has been cited extensively is [Bre01], which
describes a method for classification problems that can be adapted to regression
problems:
For building each tree, the original sample set is replaced by a set of the same size, obtained by drawing with replacement (this method is called bootstrap aggregating or bagging). At each tree node, a certain number of random features is selected (random feature selection). The sample set is splitted in two according to the values of these features, and a metric called ‘Mean Squared Error’ is computed for every split. The MSE measures the squared residuals with respect to the average value of the target variables, which could be interpreted as a measure of the sample variance. The split with the lowest MSE value is selected, and the subsamples are propagated to the children nodes. The trees grown are not pruned.
Ensemble estimators can be implemented in an embarrassingly parallel pattern.
You can do this with scikit-learn’s RandomForestClassifier using a
joblib.parallel_backend and setting the n_jobs parameter. However, you
need to be able to load your data into memory for each processor or to use
memory mapped arrays, which can be tricky specially with a distributed backend.
In our implementation, the samples as a whole are written into a binary file
and accessed using memory maps (the COMPSs runtime manages the transfers to
other nodes when needed). We used this approach because the performance penalty
of using distributed data was too large. Storing the samples file and saving
the decision trees introduces a big load to the disk storage of all nodes. If
your execution fails because you reach your disk storage limits, you can try
reducing the number of trees or reducing their size by setting the
max_depth parameter. If this is not enough, you may consider reducing
the samples.
In order to get further parallelism, each decision tree is not necessarily
built in a single task: there are tasks for building just a subtree, just a
node or even just part of a node. You can use the distr_depth parameter to
control the number of tasks used for each tree. However, be aware that the
number of tasks grows exponentially when you increase distr_depth, and that
the task loads become very unbalanced. The fitted decision trees are not
synchronized, so the prediction is equally distributed.
The results of the RandomForestRegressor can vary in every execution, due to
its random nature. To get reproducible results, a RandomState (pseudorandom
number generator) or an int can be provided to the random_state
parameter of the constructor. This works by passing a seed (generated by the
master’s RandomState) to each task that uses randomness, and creating a new
RandomState inside the task.
References:
| [Chan79] | Updating Formulae and a Pairwise Algorithm for Computing Sample Variances.
|
| [Tor99] | Inductive Learning of Tree-based Regression Models L. Torgo, 1999 Chapter 3, PhD Thesis, Faculdade de Ciências da Universidade do Porto |
Decomposition¶
Principal component analysis¶
PCA performs principal component
analysis using one of two methods: covariance and singular value
decomposition (SVD).
In the covariance method,
features are centered (the mean is subtracted for each feature) but not
standardized (not divided by the standard deviation, which would be the
correlation method). Then, the covariance matrix is estimated as x.T@x /
(n_samples - 1). Finally, the eigendecomposition of this matrix is computed,
yielding the principal components (eigenvectors) and the explained variance
(eigenvalues).
In our implementation of the covariance method, centering the features and
estimating the covariance
matrix are computed in two succesive map-reduce phases, partitioning the
samples only by row blocks. Hence, we obtain an unpartitioned covariance
matrix, of shape (n_features, n_features). This matrix is processed by a
single task which computes the eigendecomposition using the numpy.linalg
.eigh method. We can use this method, which is faster than the generic
numpy.linalg.eig, because we know that the estimated covariance matrix
is symmetric.
Our distributed implementation of the covariance method offers a good
scalability for big numbers of
samples. However, it cannot give any additional scalability with respect to
the number of features, because we hold the covariance matrix in memory and
process it as a single block. If you have
n_features >> n_samples and your data fits in memory, it may make sense
to try centering the data and then calling np.linalg.svd for equivalent
results. Lastly, bear in mind that even if you are specifying a small value
for the parameter n_components (smaller than n_features), we are still
computing the full eigendecomposition, so the fit method will not run
faster.
The SVD method is useful when n_features is large (~20,000). In
these cases, computing the eigendecomposition of the covariance matrix might
be unfeasible or take too long. The SVD method implements a block algorithm
based on Jacobi rotations [Arbenz95] and produces equivalent results to the
covariance method. This block Jacobi algorithm iteratively applies rotations
to the input ds-array directly until the eigenvectors and eigenvalues are
found. For this, some tasks of the algorithm need to load two column blocks
of the input ds-array into memory, and make use of numpy.linalg.svd
internally.
The maximum parallelism of the SVD method is limited by the number of column blocks in the input ds-array, and there is a trade-off between parallelism and task granularity. The optimal number of column blocks should not be too big or too small. If the number of features in the input ds-array is not too large, the covariance method might be more efficient.
References:
| [Arbenz95] | An Analysis of Parallel Implementations of the Block-Jacobi Algorithm for Computing the SVD P. Arbenz and A. Slapnicar, 1995 |
Model selection¶
Model selection is the task of choosing an appropriate model for your problem. This can be done by evaluating your candidate models with cross-validation, which is a technique for obtaining performance metrics with only the training data. It works by splitting your data into multiple train/validate partitions, evaluating the model obtained in each partition and aggregating the results. Model selection includes hyper-parameter optimization: selecting the best hyper-parameters (hyper-parameters are parameters that are not optimized during fitting) for your model.
The module dislib.model_selection includes 2
classes for performing hyper-parameter optimization on estimators:
GridSearchCV and RandomSearchCV. Both are very similar and use
cross-validation, differing only on how the candidate hyper-parameters are
given.
Grid search¶
GridSearchCV (grid search with
cross-validation) is a method to explore different combinations of
parameters for an estimator. It takes a grid or collection of combinations of
parameters (param_grid), and it assigns a score to each combination, so it
can be used for choosing the best set of parameters for a model
(hyper-parameter optimization). We use cross-validation, so the score is
obtained as an average of training and scoring with different
train/validation splits.
This object is very versatile: the cross-validation splitter (cv) and the
scoring method (scoring) are customizable, and multiple scorers can be
used at the same time. The results are presented in a table including, for
each combination of parameters and scorer, the scores of every split along with
the average and the standard deviation.
The splitter (cv) is an object that creates partitions of the ds-array.
This is different than in scikit-learn, where splitters partition only the
indices. We need to split the whole dataset to be able to distribute the data.
We implemented a k-fold splitter with pre-shuffling, which is the default
(with k=5).
The scoring defaults to the estimator’s score method. If the estimator
doesn’t have a score method (for example, for clustering estimators),
the user is required to provide a custom scoring.
If you use GridSearchCV with a dislib estimator, the fit and score of
all the instances will be called sequentially, so the parallelism is
achieved only through the tasks of the estimator. This limits the parallelism
if the estimator has synchronizations in its implementation (like DBSCAN),
because then each instance will not be fitted until the previous one has
finished synchronizing. This limitation can be circumvented using COMPSs nested
tasks to add another level of parallelism: having a task for fitting and
scoring each instance of the estimator. You can find an
implementation of GridSearchCV with nesting in the branch nested_search.
If you use GridSearchCV with a scikit-learn estimator, tasks are created for
fitting and scoring each instance of the estimator. This can be a solution
if the tasks of dislib estimators tasks are too fine-grained for your data.
Be aware that the data of each split is loaded to memory before calling the
fit method on scikit-learn estimators.
Randomized search¶
RandomizedSearchCV
(randomized search with cross-validation) is a method to explore different
combinations of parameters for an estimator. A given number of
combinations of parameters are sampled from distributions provided by the
user (param_distributions), and cross-validation is performed to each of
them to obtain a score.
Except for how the combinations of parameters are obtained,
RandomizedSearchCV works
exactly in the same way as
GridSearchCV, so the previous
section of the user guide applies. Randomized search has the advantage that
it may require less combinations of parameters to find an equally good result,
specially if you have some parameters that do not have a real influence on the
resulting score of predictions.